Option Charm
Option Charm indicates how much the delta will change as one trading day passes. Charm is more commonly referred to as "Delta Decay".
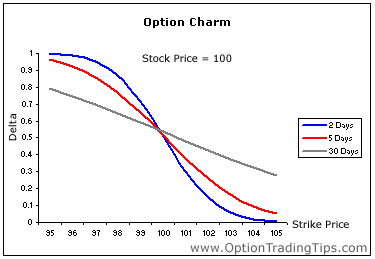
The above diagram illustrates the effect of option charm on the delta of an option. The diagram shows option delta across a series of strike prices calculated at 3 different points in time. Notice how the delta of an ITM call option approaches 1 as the option approaches expiration? And that the OTM call options approach 0 as the option nears its expiration date?
Because Option Delta is a probability estimate of the options intrinsic value, Charm is especially useful right near the options expiration date. As expiration closes in, the probability of an option that is out of the money expiring in the money decreases rapidly as each trading day passes and the option charm will estimate how much the decay will be.
The type of trader most likely to benefit from the use of option charm are those traders who use options as a hedging tool. A trader that is hedging his/her delta at the close of business may want to consider the delta decay that the portfolio will experience overnight and hence look at the charm of his/her option position.
The change in the delta will be especially evident the day before a stock goes ex-dividend.
All other things being equal, upon market open the next day the delta of the portfolio will differ by this decay. This may actually prevent the trader from over or under hedging.
The Charm value is the same for call and put options and will range in value from -1 to 1.
ITM call options and OTM put options will have positive charm values. Conversely, OTM call options and ITM put options will have negative charm. So, basically, option charm decreases as the strike price increases.
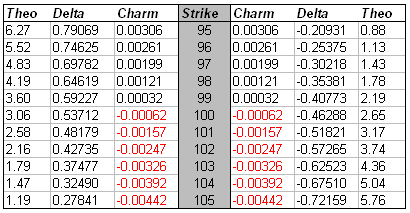
The above is a sample of what you can expect to see from Option Charm values. Notice that for ITM call options and OTM put options show positive charm, while it reverses for OTM calls and ITM puts?
PeterMarch 2nd, 2021 at 8:16pm
The image above was created using Excel. You can grab the formulas I used in my option workbook.
I don't imagine a lot of brokers would display charm in their option chains. I just checked my Interactive Brokers terminal and they don't have it.
NoobMarch 2nd, 2021 at 7:15pm
When I look at the options chain, there is no such thing as a charm value. How is this shown as?
PeterMay 10th, 2020 at 11:18pm
Hi Kyle,
Sorry, not sure I understand your question...do you mean why doesn't the Charm doesn't equal 0 for the ATM strike? If so, this is because the Charm value is calculated using the forward price, not the spot price price.
The forward price takes the spot (stock) price, adds some value for interest rates, deducts a little for the PV of any dividends to arrive at a price, which is a little higher than the spot. So, the intercept for zero will be slightly higher than the spot, or in this case, the 100 price.
Hope this helps.
KyleMay 10th, 2020 at 10:54pm
Why in the example, ATM option charm below 0(though near 0)?
Can it be explained?
PeterOctober 29th, 2018 at 12:12am
Hi Accountant,
The formulas are the same except for the negative sign before qe and d1, which reflects the change needed as calls and puts have opposite delta signs. Also, because the combined delta of a call and a put must equal 100 an increase in value of a call delta must have the exact same increase in the put delta in order for this to remain true.
accountantOctober 27th, 2018 at 9:52pm
Put charm and call charm have different analytical formulae.
I don't think you can conflate them. Reference wikipedia's greeks article.
https://en.wikipedia.org/wiki/Greeks_(finance)
Note this will need to be divided by 365 to come close to your numerical approximation.
PeterSeptember 13th, 2013 at 8:28am
Hi Eric,
Once an option expires all ITM options will have a delta of 1 and OTM deltas of 0 - so as each day passes ITM options will continue to approach 1 unless the underlying prices moves to make the option OTM.
The Y axis in the graph displays the actual delta calculated against stock price movements on the X axis. I included 3 graphs to show how delta will change with differing time-frames - i.e. approaching 1 for ITM options.
Hope this helps - let me know if anything is unclear.
EricSeptember 12th, 2013 at 3:45pm
Hi Peter,
Can you clarify why the charm approaches 1 for ITM option nearing expiration. I would think that once an ITM option is near expiration the delta is already 1, so any day that passes the delta wont change by much - i.e. it would stay at close to 1.
Is the Y axis a multiple of the previous delta? As in the Charm being 1 means the delta after 1 day is (Delta from the day before) * 1?
Really appreciate your help!
PeterDecember 27th, 2012 at 5:14am
Hi optiongeek,
Yep - I'm curious ;-) if you're ok with it I can add it to the spreadsheet.
optiongeekDecember 24th, 2012 at 8:46am
Thanks, Peter, appreciate the feedback.
By dusting off my old Calculus text (chain rule) I was able to come up with the analytic formula by differentiating the formula for delta w.r.t dt. I'd be happy to send it to you if you were curious. I haven't been able to find it anywhere else but I was able to confirm my result using Wolfram Alpha.
PeterDecember 9th, 2012 at 4:09pm
Hi optiongeek,
I didn't use a separate formula for Charm: I calculated the delta for today and then delta for tomorrow. The difference between the two is the Charm.
So if you wanted to, you could have a column for delta and then a second column for tomorrow's delta just adding one day to the date for today() should do it.
optiongeekDecember 7th, 2012 at 8:55am
Hi there, I'm looking for the analytic formula for option charm for some work I'm doing. There's something publish on the wikipedia page (Greeks (finance)) but I'm not sure I trust it. From the diagram above, you do seem to have coded up charm in excel. I looked at the spreadsheet you publish but it doesn't seem to have charm. Is there any chance you could send me the spreadsheet you used to produce the above? Thanks.
PeterAugust 29th, 2012 at 7:29pm
No, I think it makes sense that ATM charm has the lowest values as the time effect has a greater impact on OTM and ITM options.
Re: AnonymousAugust 26th, 2012 at 5:26am
If charm is delta decay, wouldn't the ATM options have the highest charm?
ATM charm is zero as delta is kept at 50.
PeterOctober 12th, 2011 at 7:16pm
If the decay was based on gamma then it would peak for the ATM options as the gamma curve also peaks ATM. However, the behavior for delta is different to gamma and doesn't have the peak in the middle at time to expiration approaches.
For ITM options the delta will increase closer to 1 (-1 for puts) as each day passes and for OTM options they approach 0. Therefore there is no peak in the curve.
AnonymousOctober 12th, 2011 at 7:35am
If charm is delta decay, wouldn't the ATM options have the highest charm?
Add a Comment