Option Rho
Rho is the change in option value that results from movements in interest rates.
The value is represented as the change in theoretical price of the option for a 1 percentage point movement in the underlying interest rate. For example, say you're pricing a call option with a theoretical value of 2.50 that is showing a Rho value of .25. If interest rates increase from 5% to 6%, then the price of the call option, theoretically at least will increase from 2.50 to 2.75.
As seen in the above graph, option rho for calls and puts have a mirrored profile; calls move from zero to a positive number as the stock price increases while puts move from a negative number towards zero under the same circumstances.
Rho, however, is more about interest rate movements than the underlying price and hence you will see greater impacts of its value depending on the premium of the option. See the next graphs.
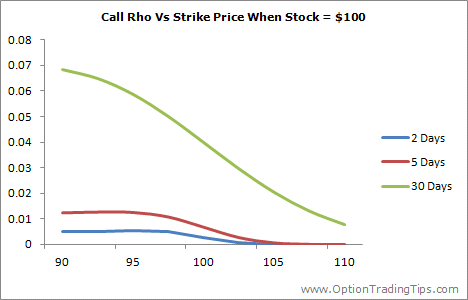
The above graphs, which plot the Rho of a call and a put option at 3 different points in time, across a range of strike prices, with a spot price of 100.
Unlike the other option greeks, Rho is larger for options that are in the money and decreases steadily as the option moves out of the money. Option Rho also increases with a greater amount of time to expiration.
These two factors are explained by the effect that interest rates have on the cost of carry of an option. ITM options, and options that have more time until expiration, will have higher premiums and therefore require more cash to hold the option until the expiration date.
Rho is generally the least important of all the option greeks. This is because option traders tend to focus on trading options that are close to expiration and out of the money.
The effect that interest rates have on option contracts is different for both call and put options.
There are two ways that interest rates affect option prices: the forward price and the premium discounting.
Forward Price
When calculating the price of an option, the first thing traders have to determine is what the price of he underlying asset will be at the expiration date. This is known as the forward price. Although an option trader can never know what this price will be, all other things being equal, it must be worth at least the cost of holding the asset until the expiration date. This value takes into account the cost of money i.e. what it would cost you in real terms to borrow and invest in the asset until the expiration date. This value, also refered to as the "cost of carry", uses the current interest rate to determine how much additional capital you will need to hold the asset until the expiration date.
Take a look at this spreadsheet to see how the forward price is calculated:
For call and put options, the cost of carry has different effects on the price of the option. As interest rates increase, the forward price of the asset also increases, however, the effect on the option premium differs for calls and puts. For call options, the premium of the option increases as the forward price increase, but for put options the premiums decrease as the forward price increases. As interest rates decrease, call options will decrease in value and put options will increase with changes in the forward price.
Discounting Factor
The second way that interest rates effect the pricing of option contracts is in the discounting of the premium.
The price of an option contract is a future value. I.e. it estimates what the value of the instrument will be at some date in the future.
So, when you buy an option contract you are outlaying money today in order to receive some value in the future. When you do this you have to consider what this investment is going to cost you over the life of the option.
In other words,what is the value of the option in today's terms?
To calculate this, we do what is called discounting or calculating the present value of the option. Here's a spreadsheet to illustrate.
It basically comes down to the finance principle "a dollar today is worth more than a dollar tomorrow".


annaFebruary 16th, 2017 at 9:14am
Hi,
Could someone explain how the conversions/reversals would hedge Rho ?
I didn't understand why ..
Thank you !
PeterSeptember 12th, 2016 at 12:13am
Hi Waqar,
You're right...I hadn't thought of conversions/reversals for a hedge. Because a puts Rho is positive, buying a call and selling a put increases your Rho exposure. Thanks!
Waqar. September 6th, 2016 at 2:58pm
you cant hegdge the Rho ascpet with just naked calls and outs, Rho expousre of the option can be hedged with Conversion, Reversals, Boxes and jelly roll. After you discren the source of your interest component.
PeterMarch 26th, 2012 at 8:08pm
Hi Bubuwanted,
Because a stock will have a zero Rho, you can only hedge out Rho with another option.
bubuwantedMarch 21st, 2012 at 4:10pm
let's assume we're long a put. How do we hedge the rho? which product to use?
thanks!
PeterDecember 6th, 2011 at 9:45pm
No, they are correct - the two graphs for call and put are plotting Rho per strike on the x-axis - not one Rho vs underlying price.
I see your point though - it is confusing that way.
I've now added a new graph above showing Rho vs underlying price.
Thanks for the suggestion!
JoeyDecember 5th, 2011 at 6:31am
You got the slope of the rho for call wrong, rho for call should be postively sloped
PeterSeptember 20th, 2010 at 1:49pm
Rho is all about cash flows. A futures contract doesn't require cash outlay as they are margined and the amount deposited earns interest, so a change in interest rates will have a zero effect on both calls and puts based on a futures contract.
Calls on a stock, however, will have a positive Rho as a rise in interest rates means a call option will be relatively cheaper to own then the underlying stock and vice versa for the put options, which have a negative Rho.
StefanSeptember 20th, 2010 at 9:44am
The interesting thing is, that for an option on a future both call and put have the same sensitivity to rho.
So why should they have different sensitivities if the Underlying is the cash instrument?
If you follow a stock valuation approach like e.g. DCF and consequently replace the stock price S in your Option Pricing formula by the discounted forward an increasing interest rate will no longer push the forward higher, but will drive the underlying price down (this is actually what we all observe when interest rates go up, don't we?)
DichyMarch 3rd, 2010 at 12:36pm
Increasing rates will push push forwards higher, and reduce discount factor. So for calls two effects are opposing, and for puts the two effects work together. So puts are more sensitive to rates.
PuchyMarch 3rd, 2010 at 12:32pm
No Ashi.
PeterDecember 23rd, 2009 at 4:37pm
It would depend on the volatility, time to expiration, interest rates and dividends. If you have those factors, you can enter them into my spreadsheet to calculate Rho;
https://www.optiontradingtips.com/pricing/free-spreadsheet.html
neerajDecember 18th, 2009 at 9:20am
how we claculat option primium if underlying assets 5000 so
how much primium for 4600 put
PeterNovember 16th, 2009 at 4:01am
No, it's only Gamma and Vega where the sensitivities for calls and puts are the same. Take a look at my spreadsheet under the Pricing link and you can see how Rho changes for calls and puts at different strikes.
AshiNovember 14th, 2009 at 5:16pm
Does a call and a put have equal sensitivity to rho?
Add a Comment