An option is a financial derivative whose value is determined by the value of another asset (called the underlying).
Index options are calls or puts where the underlying asset is a stock market index i.e the Dow Jones or the S&P 500 index. Using index options enables option traders to bet on the direction or volatility on an entire equity market (or market segment) without having to trade option on all of the individual securities.
The most popular index option markets are:
| Symbol | Description | Country |
|---|---|---|
| KOSPI | KOSPI 200 Index Options | Korea |
| DAX | DAX 30 Index Options | Germany |
| SPX | S&P 500 Index Options | USA |
| NDX | NASDAQ 100 Index Options | USA |
| OEX | S&P 100 Index Options | USA |
| HSI | Hang Seng Index Options | Hong Kong |
| N225 | Nikkei 225 Index Options | Japan |
| FTSE | FTSE 100 Index Options | UK |
According to the Futures Industry Magazine the KOSPI was the largest in volume (number of outright contracts) during 2008. I would say though that the OEX, SPX and NDX are the biggest in terms of market capitalization. OEX, SPX and NDX options are all traded on the CBOE.
Generally, the factors for the pricing of index options are the same as equity options with a European exercise. I.e the inputs of underlying price, strike price, interest rate, volatility, dividend, call or put are fed into the Black and Scholes pricing model to calculate the premium.
The main difficulty for traders pricing index options is the dividend estimate.
To calculate the dividend component correctly, an option trader will need to know all of the individual stock component dividends and weight them in proportion to each stocks weighting in the index basket. Large investment banks and hedge funds will have a research division to carry out this task. However, another way is to use a 3rd party source like Bloomberg who publishes the dividend yield for the index as calculated from all of the component stocks.
One way that I've seen trader's workaround this is to not use any dividend estimates at all and instead base their options on the front month futures contract (instead of the index itself) to determine the theoretical forward of the option. This works well for front month options based off a front month future. For back month options, traders will use the front month future as the base contract and apply an "offset" to the forward price used to reflect the carry cost from the front month to back month. Traders usually use the futures roll price from the front month to back month to determine this carry cost.
With this method index option traders are assuming that the index futures contract has already priced the dividends into the futures market price.
Almost. There are a few exceptions, like the OEX (CBOE: OEX), which are cash settled American style index options. A trader may exercise OEX options at any time prior to the expiration date and the amount to settle will be based upon the closing price of all of the component stocks on the day the trader exercises.
An American style index option with a physical settlement would be a nightmare for option clearing houses. Say you were long a call option on the S&P 500 index and decided during the day to exercise. Your broker would have to arrange with the clearing house for delivery of all 500 stocks in their correct weighting and price at the time of exercise to you. And the seller would then be short all 500 stocks.
One exception to this is the SPI. SPI options (Australian All Ordinaries Index) are referred to as index options, however, they are technically "futures options" as the underlying security for the options is the SPI future. SPI options are American exercise and exercise into the appropriate futures contract.
Most index options are serial: March, June, September and December. The exceptions (AFAIK) are the Hang Seng and the KOSPI. HSI and KOSPI have options every month for the first 3 consecutive months and then serial months thereafter.
As most index options are European exercised (exceptions are SPI/OEX) where physical delivery is not possible, settlement is always done in cash and will occur on the next business day after exercise.
Determining the settlement price differs from index to index and option traders will need to refer to the contract specifications to be sure what method will be used to determine the price.
For example, the settlement price used for the options on the KOSPI index is determined by the weighted average price of all of the component stocks in the last 30 minutes of trading on the final trading day. The NIKKEI 225 index options are settled according to the weighted average of the opening price of all of the component stocks the morning "after" the final trading day. Options on the FTSE index are settled basis the Exchange Delivery Settlement Price (EDSP) as reported by LIFFE on the last day of trading.
Index option traders eagerly await the final settlement price, which is reported by the exchange. It is referred to as The SQ (which I believe is Settlement Quote. I've also heard it referred to as Special Quotation...I'm not sure which expansion is correct).
Another type of index option that is very popular to trade are options on Volatility Indexes.
More on Volatility Options.
Options based on indices rather than individual stocks provide investors with diversification.
In finance, a text book will tell you that diversification means the removal of unsystematic risk. However, if you've ever come across the saying “don’t put all your eggs in one basket” then you have already been introduced to the concept of diversification. It basically means spreading your investment across multiple assets, in this case, multiple stocks with the objective of reducing (or evening out) your overall risk.
A stock index is a compilation of many stocks. The S&P 500 is meant to resemble a portfolio made up of 500 individual companies. Index options based off the S&P 500 (SPX) give option traders the chance to construct option strategies and techniques to bet on the entire market rather than the performance of one individual stock.
I don't mean to mention that index options are easy to predict. But index options are generally less volatile than the component stocks that make up the index.
Earnings reports, takeover rumors, news and other market events are what drive volatility in individual stocks. An index tends to smooth out the wild ups and downs of the stock basket and hence options based off an index will also show lower fluctuations.
Index options are very popular for option traders, hedge funds and investment firms. This popularity drives up the volumes available to trade and reduces the spreads quoted in the market. This competition means that you will always have a fair price to trade at and plenty of volume too.
http://www.amex.com/options/eductn/op_edu_whatIs_index_pg1.html
http://financial-dictionary.thefreedictionary.com/Index+option
PeterMay 27th, 2019 at 7:13am
By uncovered do you mean calculating without knowing what the index dividend is?
JumpyMay 9th, 2019 at 7:00am
ok... any suggestion from you about this still uncovered scenario?
Thanks and regards
PeterApril 30th, 2019 at 7:13pm
Hi Jumpy,
Yes, correct, q is no longer an independent variable.
The r < 0 having physical meaning is unclear to me. Typically, the r value represents the value of money if not invested. I.e. if you didn't buy/sell risk assets such as options/stocks, what is the value of your money if simply left with a risk-free alternative?
If interest rates are negative in Europe, what happens to your money if left in one of these assets, such as a bank? Are you left with less money in the future due to negative interest rates? I don't know the answer to this. Perhaps not. If you are deducted interest on your money, then yes you should enter a negative value for r. However, if your money simply stays flat then enter 0 for r.
The reason for using the offset for back months and having the main price of the front month futures is for hedging. Front month futures have the most liquidity and offer tighter bid/ask spreads than back month futures providing a better alternative for hedging option positions. So if pricing an option in a back month where there is indeed a corresponding futures contract, the forward price would use the front month as the base and the difference between the two futures contracts as the offset. However, you're of course welcome to use the back month future as the forward price if you think the liquidity is acceptable.
For months without futures contracts, then yes, you are back to the same problem of needing to find out what the dividend value is.
AnonymousApril 30th, 2019 at 4:32am
Hi Peter,
When I say "the q variable is not required anymore" I mean that variable is no more an independent variable, because I can set q = r, so only r remains an independent variable I need to find somewhere.
I spoke about negative interest rate because the better proxy of r I tought is the Euribor (please see the link into my comment below), valued at the right time interval. If I've a 3 months expirying Option, then I use a 3 months Euribor and so on.
A reason why I asked for you which source you consider better to value the risk free rate, is just it. I don't know if having r <0 it has an any phisical meaning in this context.
If you have to calculate the price for and European style index option (ex. Eurostoxx50, S&P500, FTSE MIB, etc...) using the B&S model, which proxies and relative source links (if more than one for the different above mentioned indexes are available) do you suggest for r value?
If you say "if you don't have a futures price for the options month then you cannot use this method reliably for estimating the forward price. You would then need to find a source to provide a dividend yield amount and use that for q.",
in other words, you mean I have to go back to the start of the problem, while in the post it seems you suggest another way.
Infact you write "One way that I've seen trader's workaround this is to not use any dividend estimates at all and instead base their options on the front month futures contract (instead of the index itself) to determine the theoretical forward of the option...
... For back month options, traders will use the front month future as the base contract and apply an "offset" to the forward price used to reflect the carry cost from the front month to back month. Traders usually use the futures roll price from the front month to back month to determine this carry cost." Could you explain, better with an example, what you mean?
Instead, in the case I have a futures price for the options month, I have no problems because no "offset" is required and with the futures price I have directly the best proxy for the index forward value at expiry.
Thanks a lot for your quick response and for the possibility to share our reasonings
PeterApril 28th, 2019 at 10:15pm
Hi Jumpy,
Yes, you're right, q = r. However, this doesn't mean that you should just put zero; you still need r, which is needed to discount the premium to today's value. And yes, because you've made the spot the forward price, there is no need for the q (dividend estimation).
Negative interest rates? I'm not sure how best to handle that. This would imply a negative forward price, which means you need to pay a bank to keep your money, rather than receiving interest from the bank. Is this what happens?
Yes, if you don't have a futures price for the options month then you cannot use this method reliably for estimating the forward price. You would then need to find a source to provide a dividend yield amount and use that for q.
JumpyApril 26th, 2019 at 1:56pm
Hi Peter,
thanks for your answer...
I think I understood the "hack" of B&S model... it is based on Spot-Future parity equation, F = S * e^(r-q)t
If I set q = r, for each t, I have S = F so I can hake the model using F instead of S as Underlying input variable.
Is it right?
If it is so, the q variable is not required anymore in the model and I need to worry only about risk free rate estimation.
Is it right?
What is the source you recommend for risk-free rate estimation in case of European stocks/indexes?
is it right to refer to the Euribor (https://www.euribor-rates.eu/current-euribor-rates.asp) or what else?
In case of negative interest rates, do I have to use that negative value in any case or use 0 value?
Regarding "Let me know if this doesn't make sense. I may write up a more detailed example as a new article to explain further." --> I think it could be very usefull if you made a more detailed/numeric example on Eurostoxx50 (option with expiry date equal to May). It would be really useful for better understand what you mean with front month and next month futures and if I can really calculate the difference you are speaking about "This offset you can calculate by subtracting the next month future from the front month". If I have future's quotations only for Mar, Jun, Sep, Dec, how can I find the future price for front month and the next month of the front month?
I suppose there is something wrong with my reasoning
Thanks and regards
PeterApril 25th, 2019 at 7:50pm
Hi Jumpy,
The BS model takes the raw underlying price (spot) and adjusts this to create a forward price using both interest rates and dividends.
If you are valuing index options where there are futures contracts and you do not know what the dividends are for the stocks in the index, then another way to price the options is by using the futures price instead of the index price as the underlying price input.
If you assume that the markets are efficient then the futures price serves as a proxy for the index forward for the same expiration date.
Typically, you would use a different pricing model for this e.g. Black76 or other options on futures models.
However, you can also "hack" the Black and Scholes model to do the same thing.
To do this, you enter the front month futures price as the underlying price. Then, whatever rate you have as the interest rate, use this same rate in the dividend yield input. Doing this keeps the raw futures price as the input to the model while still using the interest rate for discounting the option premium.
For back month options, the offset I mentioned is the difference in forward price between the front month future and the next month future. This offset you can calculate by subtracting the next month future from the front month. This offset value is added to the underlying price to create the synthetic forward price for the month of options you are trying to evaluate.
Let me know if this doesn't make sense. I may write up a more detailed example as a new article to explain further.
JumpyApril 23rd, 2019 at 9:31am
Hi Peter,
first of all thanks for all the info provided in your website.
Just to see if I'm correct in understanding index option's modeling by extended B&S formulas (dividend yield contribution added), in case of index's dividend payment (future price different from spot price).
Ex.
In order to forecast Call and Put option's price, if I have EUROSTOXX50 options, how can I input B&S model?
i) option's expiry date = future's expiry date (Mar, Jun, Sep, Dec)
my proposal (only relevant inputs for my understanding) for Call/Put options expiring at Jun'19:
- underlying price = future@Jun'19 price, strike price = strike price w/o any adjustments, rf-rate = -0.34 risk-free cash rate (average of rf-rate to 1 month = -0.37 and rf-rate to 3 month = -0.31), div yield = 0)
ii) option's expiry date <> future's expiry date (other than Mar, Jun, Sep, Dec)
my proposal (only relevant inputs for my understanding) for Call/Put options expiring at Jul'19:
- underlying price = future@Jun'19 price + OFFSET, strike price = strike price w/o any adjustments, rf = rf-rate = -0.34 risk-free cash rate (average of rf-rate to 1 month = -0.37 and rf-rate to 3 month = -0.31), div yield = 0)
Could you do same examples about OFFSET calculation as you wrote in this web page above? or suggest how to be correct in B&S modelling?
This is the link I use for the risk-free rate:
Is it correct? If not, could you suggest a different data source?
Note: sorry for my probably poor english, but I'm not a native english
Thanks and regards
PeterJanuary 15th, 2017 at 7:53pm
Hi Dean,
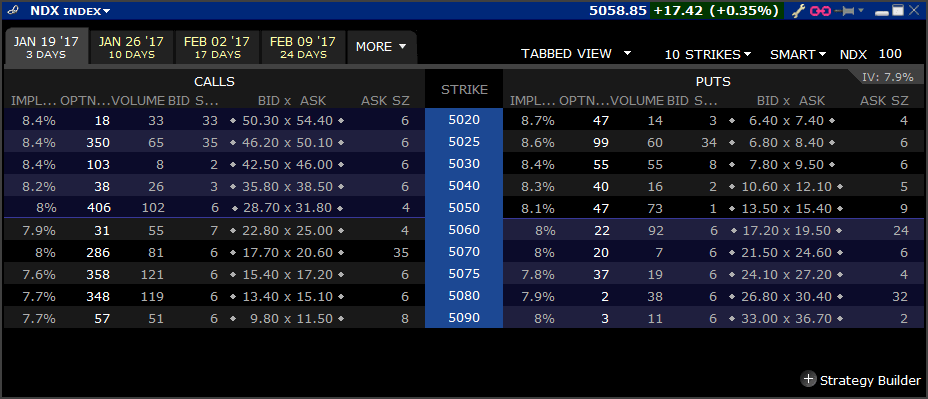
You can trade both of these products using Interactive Brokers. Here is a screen shot of the NASDAQ options just now:
I can't show DAX as I haven't subscribed to receive DAX market data.
I've emailed you also.
DeanJanuary 15th, 2017 at 1:09am
Hi,
Im looking to trade european style options like dax and nasdaq. Which broker provides the products. Can i see the options chain on the exchange website. Im a small investor and Im not interested in binary options. Can you please send me the details to my email address: [email removed ]
PeterFebruary 8th, 2011 at 4:29pm
Hi Paul,
MSFT is one of about 40 stocks that now have weekly options available to trade. As soon as they are listed they have approximately one week until expiration.
February 11 is the normal series expiration and February 19 is the weekly date.
Here's a link to read more about Weekly Options.
PaulFebruary 7th, 2011 at 4:30am
Hi Peter,
I am looking at option symbols at the moment. For MSFT I noticed that there seem to be two expiration dates e.g. MSFT110219 and MSFT110211. What is the significance of each of these dates - is the 11th the expiration date and the 19th is the date by which the broker will pay any profit due? Thanks.
JesseOctober 4th, 2010 at 2:27am
Hi Peter,
Thanks again for your reply and suggestion.
PeterOctober 3rd, 2010 at 9:09pm
There's also "The Index Trading Course" by George Fontanills and "Trading Index Options" by James Bittman. I've not read these so cannot comment directly.
JesseOctober 3rd, 2010 at 7:56am
Hi Peter,
Thanks for your prompt reply. Yes, I've already had Natenborg's book plus Charles Cottle's Options Trading: The Hidden Reality. At the moment, I'm trading stock options only, still not confident enough in dabbling into index option trading.
PeterOctober 3rd, 2010 at 4:56am
Hi Jesse, have you looked at Option Volatility & Pricing
 ? Many option traders refer to it as the Bible of option trading...it discusses options a most asset types.
? Many option traders refer to it as the Bible of option trading...it discusses options a most asset types.
JesseOctober 2nd, 2010 at 9:06pm
Hi Peter,
Thanks for the info provided in your website, it's very useful. Btw, I've done some amazon searches for a good practical index option trading book, but it seems that most of the bookds are related to stock options, can you recommend one that's updated and practical?
Thanks again
PeterFebruary 24th, 2010 at 4:42pm
Thanks for the feedback Tom. I've updated the content accordingly.
TomFebruary 24th, 2010 at 7:31am
All index options are not European. The OEX is American style. It is cash settled, so if you exercise an in the money call, you get the market price minus the strike price * $100
PeterJune 14th, 2009 at 1:45am
Hi Ainsley,
I think this is because ETF's often pay dividends. Having options that are American style gives the call option holders the opportunity to exercise before expiration and take up the dividend.
ainsleyJune 13th, 2009 at 11:55pm
please explain why ETF OPTIONS styles are usually american and not european.
Add a Comment